TEMA 4: TESELADOS. - Arte y Matemáticas en la Geometría

 

Introducción

Los teselados son formas de recubrir un plano sin dejar espacios ni superposiciones, utilizando figuras geométricas que se repiten. Los vemos en los pisos de cerámica, mosaicos, vitrales, panales de abejas e incluso en obras artísticas de Escher. Comprender cómo funcionan los teselados nos ayuda a conectar la geometría con la arquitectura, el arte y la naturaleza.

1️⃣ Conceptos clave

👉 Teselado: recubrimiento del plano mediante figuras geométricas repetidas sin dejar huecos ni superponerse.

👉 Teselado regular: formado por un único tipo de polígono regular (ej. triángulos equiláteros, cuadrados o hexágonos).

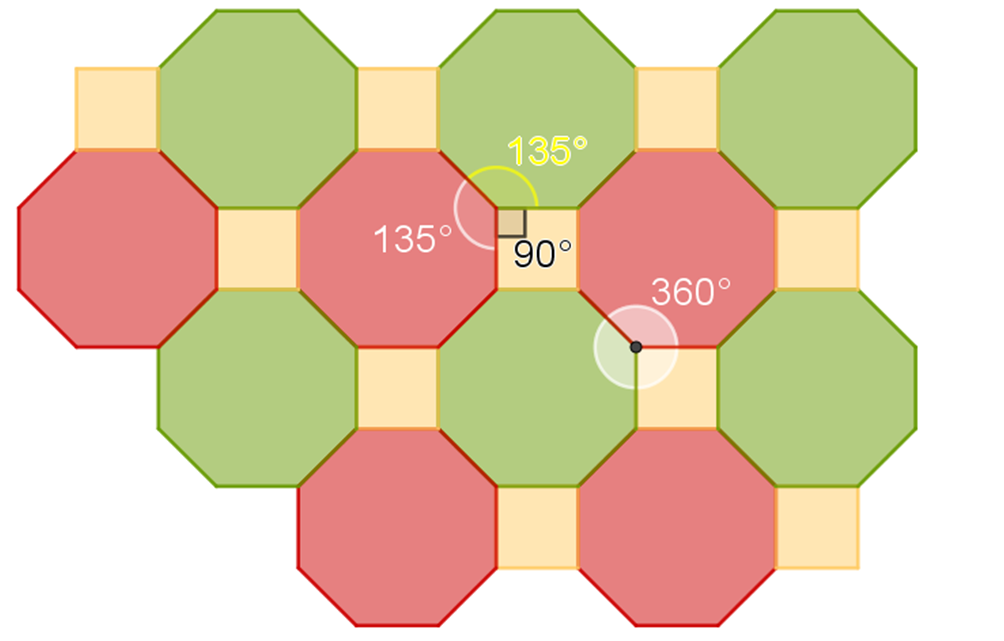
👉 Teselado semirregular: combina dos o más tipos de polígonos regulares en un mismo patrón.

👉 Condición para un teselado:

La suma de los ángulos que se encuentran en un vértice debe ser 360°.

2️⃣ Ejemplos

🔹 Ejemplo 1: Teselado con triángulos equiláteros.
Cada ángulo mide 60°.
En un vértice se juntan 6 triángulos:

$$6 \times 60° = 360°$$

👉 Sí se forma un teselado.

🔹 Ejemplo 2: Teselado con pentágonos regulares.
Cada ángulo mide 108°.
Si intentamos juntar 3 en un vértice:

$$3 \times 108° = 324° < 360°$$

👉 Queda espacio.
Con 4 pentágonos:

$$4 \times 108° = 432° > 360°$$

👉 Se sobrepasa.
Por lo tanto, los pentágonos regulares no forman teselados regulares.

3️⃣ Actividades

Actividad 1. Conceptos
En tu cuaderno, escribe la información de conceptos clave que aparece en la parte superior de este blog.

Actividad 2. Identificación
En tu cuaderno, construye los ejemplos de polígonos anteriores y determina si pueden formar teselados regulares de forma geométrica, así mismo construye y comprueba con los siguientes polígonos regulares:

• Cuadrado

• Hexágono

• Octágono

Actividad 3. Construcción de teselados simples
Con regla, transportador y colores, construye al menos dos teselados regulares en tu cuaderno (ej. triángulos y cuadrados). Pinta las figuras de diferentes colores para resaltar el patrón.

Actividad 4. Teselado semirregular
Investiga qué combinaciones de polígonos permiten cubrir el plano (por ejemplo, cuadrados y triángulos). Elige una y construye el patrón en tu cuaderno.

4️⃣ Autoevaluación

Marca con una ✅ lo que lograste en este tema:

• Sé qué es un teselado y sus tipos.

• Puedo identificar qué polígonos regulares forman teselados.

• Construí al menos dos teselados regulares en mi cuaderno.

• Reconozco aplicaciones reales de los teselados en la vida diaria.

Archivo descargable con actividades: Da clic aquí.