TEMA 2: Polígonos y sus ángulos. "Construcción de polígonos regulares"

 

Introducción

Los polígonos están presentes en muchísimos objetos de nuestra vida cotidiana: desde las señales de tránsito (triángulo de precaución, octágono de “alto”) hasta los mosaicos de los pisos y los paneles de un balón de fútbol. Comprender sus lados, ángulos y cómo se construyen es fundamental en matemáticas y en el diseño arquitectónico o artístico.

En esta semana aprenderemos a identificar, calcular y construir polígonos regulares, sentando las bases para los teselados que veremos más adelante.

1. ¿Qué es un polígono?

Un polígono es una figura cerrada formada por segmentos de recta que se unen en sus extremos.

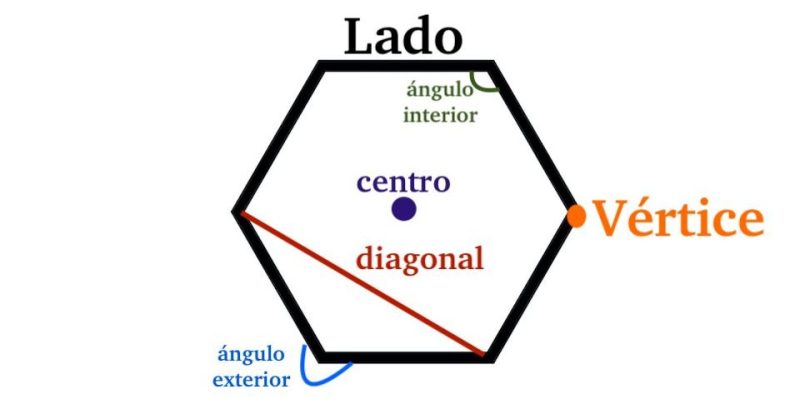
• Cada segmento se llama lado.

• Los puntos donde se unen los lados son los vértices.

• La abertura que forman los lados en cada vértice son los ángulos interiores.

2. Clasificación de polígonos

Según su número de lados:

• 3 lados → Triángulo

• 4 lados → Cuadrilátero

• 5 lados → Pentágono

• 6 lados → Hexágono

• 8 lados → Octágono, etc.

👉 Si todos sus lados y ángulos son iguales, se llaman polígonos regulares.

Ejemplos: triángulo equilátero, cuadrado, pentágono regular, hexágono regular.

3. Ángulos de un polígono

La suma de los ángulos interiores de un polígono depende de cuántos lados tenga.
La fórmula es:

$$S = (n - 2) \times 180^\circ$$

donde n = número de lados.

👉 Ejemplo: Para un pentágono (5 lados):

$$S = (5 - 2) \times 180^\circ = 3 \times 180^\circ = 540^\circ$$

Cada ángulo interior en un polígono regular se calcula dividiendo la suma entre el número de lados:

$$$$Aˊngulo interior=Sn​

👉 Ejemplo: En un pentágono regular:

$$\frac{540^\circ}{5} = 108^\circ$$

4. Construcción de polígonos regulares

a) Con transportador

1. Dibuja un círculo.

2. Divide la circunferencia en partes iguales según el número de lados.

3. Une los puntos marcados para formar el polígono.

👉 Ejemplo: Para un hexágono (6 lados), divide el círculo en 6 partes de 60° cada una.

b) Con compás

• Para un hexágono:

• Traza un círculo con radio $r$.

• Con el mismo radio, marca sobre la circunferencia seis puntos consecutivos.

• Une los puntos → obtienes un hexágono regular.

Ejercicios de práctica

Ejercicio 1: Clasificación y construcción

Dibuja y nombra los siguientes polígonos:

1. Triángulo

2. Cuadrado

3. Pentágono

4. Hexágono

5. Octágono

Ejercicio 2: Suma de ángulos interiores

Calcula la suma de ángulos interiores en:

1. Un cuadrado

2. Un pentágono

3. Un hexágono

4. Un octágono

(Pista: usa la fórmula $S = (n-2)\times 180^\circ$.

Ejercicio 3: Ángulo interior de polígonos regulares

Encuentra el valor de cada ángulo interior en:

1. Un triángulo equilátero

2. Un pentágono regular

3. Un hexágono regular

4. Un octágono regular

Conclusión de la Semana 2

En esta semana aprendimos a:

• Identificar polígonos y clasificarlos por sus lados.

• Calcular la suma de ángulos interiores y el valor de cada ángulo en polígonos regulares.

• Construir polígonos regulares con transportador y compás.

FICHA DESCARGABLE CON LAS ACTIVIDADES: DA CLIC AQUÍ